imhamburger 님의 블로그
[자료구조] 이진 탐색 트리 (Binary Search Tree) 본문
이진트리는 자식 노드가 최대 두 개인 노드들로 구성된 트리이다.
그래서 이진 탐색 트리는 뭐야?
이진 탐색 트리는 이진 트리에서 어떠한 규칙에 따라 나열된 트리이다.
- 규칙1: 모든 왼쪽 노드는 부모노드보다 값이 작거나 같다.
- 규칙2: 모든 오른쪽 노드는 부모노드보다 값이 크다.
그럼 파이썬으로 구현해보자.
#이진 탐색 트리의 노드를 나타내는 클래스
class Node:
def __init__(self, key):
self.key = key
self.left = None
self.right = None- key: 노드의 값
- left: 왼쪽 자식 노드
- right: 오른쪽 자식 노드
Insert 함수
class BinarySearchTree:
def __init__(self):
self.root = None
#트리에 새로운 값 삽입
def insert(self, key):
if self.root is None:
self.root = Node(key)
else:
self._insert(self.root, key)
#재귀적으로 트리에 값을 삽입
def _insert(self, current_node, key):
if key < current_node.key:
if current_node.left is None:
current_node.left = Node(key)
else:
self._insert(current_node.left, key)
elif key > current_node.key:
if current_node.right is None:
current_node.right = Node(key)
else:
self._insert(current_node.right, key)
else: pass- pass는 중복된 값은 허용하지 않기 때문에.
Search 함수
#트리에서 특정값 검색
def search(self, key):
return self._search(self.root, key)
def _search(self, current_node, key):
if current_node is None:
return False
if key == current_node.key:
return True
elif key < current_node.key:
return self._search(current_node.left, key)
else:
return self._search(current_node.right, key)
inorder_traversal 중위순회 함수
def inorder_traversal(self):
result = []
self._inorder_traversal(self.root, result)
return result
def _inorder_traversal(self, current_node, result):
if current_node is not None:
self._inorder_traversal(current_node.left, result)
result.append(current_node.key)
self._inorder_traversal(current_node.right, result)- inorder는 왼쪽자식 -> 현재노드 -> 오른쪽 자식 순서로 탐색
순회란?
이진트리 노드의 key값을 빠짐없이 출력하는 방법이다.
- preorder: M -> L -> R (루트 -> 왼쪽 -> 오른쪽)
- inorder: L -> M -> R
- postorder: L -> R -> M
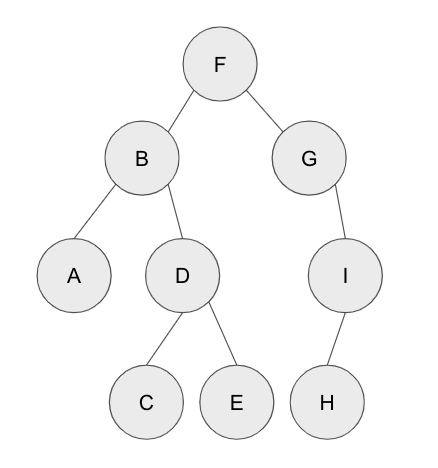
preorder: F B A D C E G I H
inorder: A B C D E F G H I
postorder: A C E D B H I G F
delete 함수
def delete(self, key):
self.root = self._delete(self.root, key)
def _delete(self, current_node, key):
if current_node is None:
return current_node
if key < current_node.key:
current_node.left = self._delete(current_node.left, key)
elif key > current_node.key:
current_node.right = self._delete(current_node.right, key)
else:
#하나의 자식 노드 또는 자식 노드가 없는 경우
if current_node.left is None:
return current_node.right
elif current_node.right is None:
return current_node.left
temp = self._min_value_node(current_node.right)
current_node.key = temp.key
current_node.right = self._delete(current_node.right, temp.key)
return current_node
def _min_value_node(self, node):
#서브트리에서 최소값 노드 반환
current = node
while current.left is not None:
current = current.left
return current
'알고리즘(Algorithm)' 카테고리의 다른 글
| [자료구조] 그래프 (Graph) (0) | 2025.02.04 |
|---|---|
| 자료구조, 그것이 알고싶다. (0) | 2025.01.26 |
| 프로그래머스 DFS 문제풀이 - 여행경로 (0) | 2025.01.11 |
| 프로그래머스 다익스트라 문제풀이 - 가장 먼 노드 (0) | 2024.11.07 |
| 알고리즘(Algorithm) - 정렬 알고리즘 개념 이해와 구현하기 (+재귀함수) (0) | 2024.09.01 |


